ITパスポートの【テクノロジ系】に分野について学習を進めていきましょう!
基礎理論としてコンピュータの世界での数値の数え方や論理演算について、基本的な部分を学習する必要があります。
私たちの日常に馴染みがある『10進数』の他にも『2進数』、『16進数』などについて理解する必要があり、その表記法の変換について学習することが、ITパスポート試験では重要となります。
コンピュータの世界で使用される『2進数』の論理演算などについても、しっかりと学習し、理解を深めていきましょう!

表記法について
10進数
値が10になるときに桁が一つ上がる表記法
一般的に日常的に使用されている表記法
2進数
値が2になるときに桁が上がる表記法
コンピュータの世界では基本的に、電圧の低い状態、高い状態を2進数で処理される
16進数
値が16になるときに桁が上がる表記法
アラビア数字0~9に加え、アルファベットのAからFまでを使って表現する
基数
桁上がりの基準となる数
10進数の基数は『10』となり、2進数の基数は『2』、16進数の基数は『16』となる。
基数変換の方法
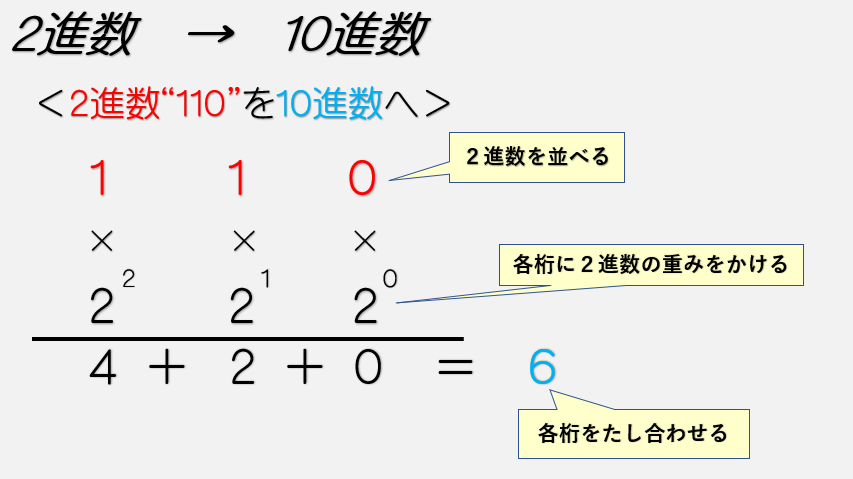
2進数 → 10進数
各桁の数字 × 2ⁿ (nは[ 桁数-1 ])
計算したあとにかけ算した数字をたし算する。
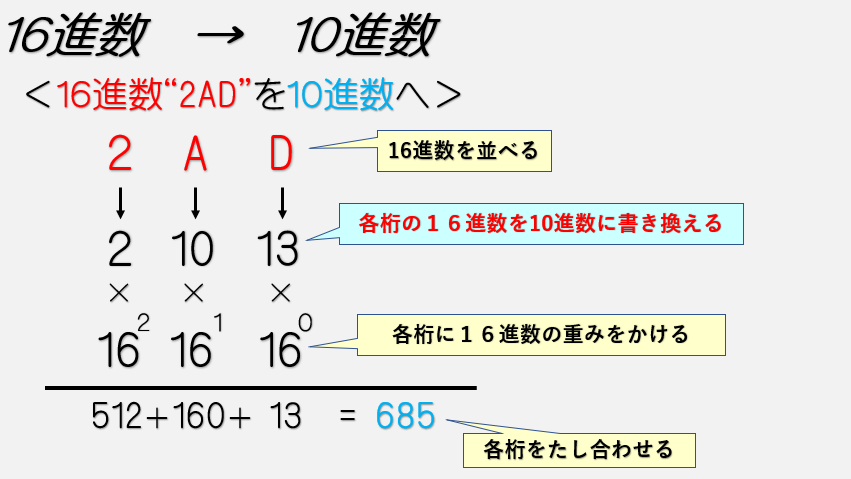
16進数 → 10進数
16進数のアルファベットを10進数に変換する。
各桁の数字 × 16ⁿ (nは[ 桁数-1 ])
計算したあとにかけ算した数字をたし算する。
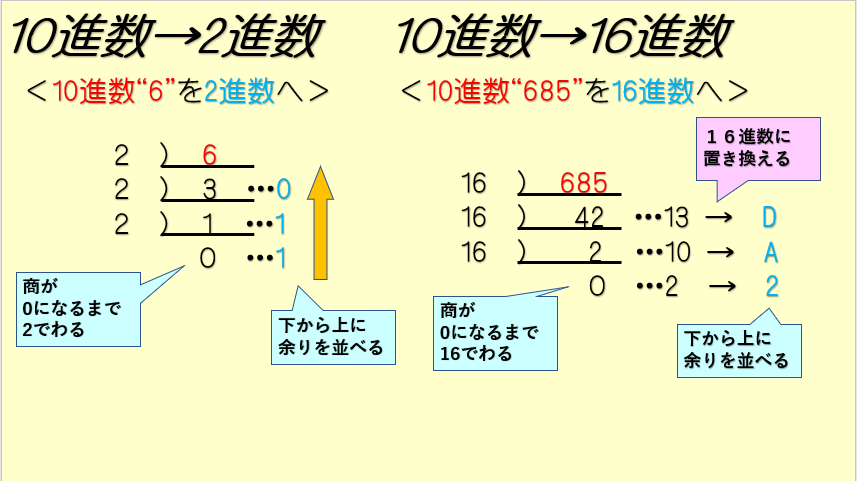
10進数 → 2進数 / 16進数
論理演算について
集合
はっきりと区別できる条件で、グループわけされたものの集まり
この集合を構成するものを『要素』とゆう。
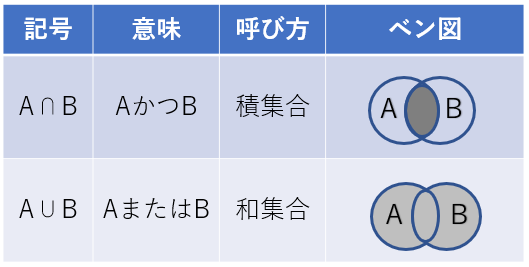
ベン図
集合の関係を視覚的に表した図
⋂(キャップ)は『かつ』を表す、⋃(カップ)は『または』を表現している。
部分集合
集合Aの要素が、集合Bの一部、もしくは全部になっているとき、『AはBの部分集合である』と表現する。
論理演算子(真理値表)
コンピュータの世界は2進数で表現されるため、コンピュータに計算させるために応用された演算方法
OR(論理和):AとBの少なくとも一方が『1』の場合に、答えが『1』となる論理演算
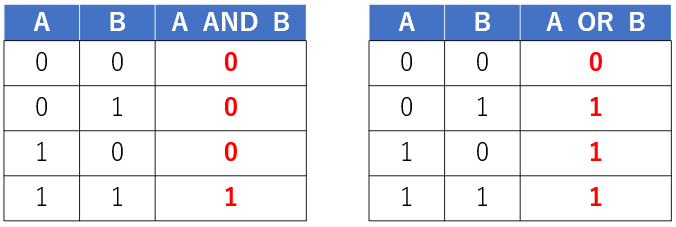
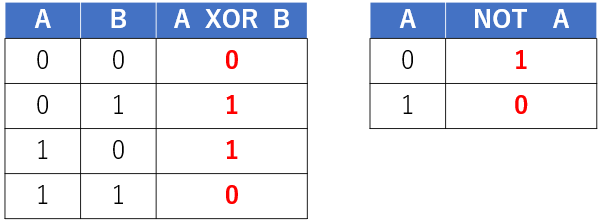
NOT(否定):入力の反対となる論理演算
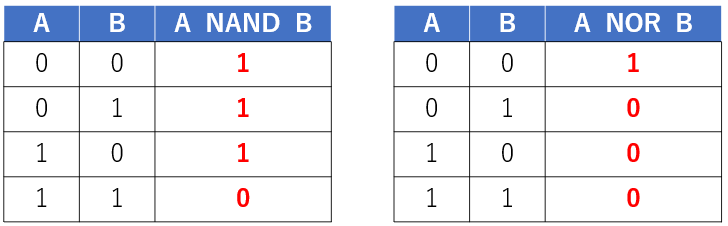
NOR(否定論理和):論理和と否定を組み合わせた論理演算

・『10進数』を『2進数』、『16進数』に変換する方法や、その逆の変換方法をしっかりと身に付けましょう!
・さまざまな論理演算について内容を理解し、『真理値表』を確実にマスターしましょう。




コメント